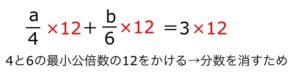分数を使った等式の変形のやり方がわからない、、、
等式の変形好きですか?嫌いですよね、難しいですよね。
特に分数が入ってると「どうやってやればいいの?」と思ってしまいますよね?
今日はその分数を使った等式の変形の解き方、やり方を教えていきます。
分数を使った等式の変形の解き方のコツ
邪魔な分数をかけ算で消しちゃう
[]内の文字について解きなさい
分数が邪魔なので、まずは分数を消してしまいましょう。
4と6を消すためには、最小公倍数である12をかける必要がありますね。
なので分数が2と3なら6倍、2と7なら14倍のようにまず最小公倍数をかけましょう、
かけ算をおこなうと、このような式になります。
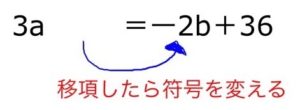
そしてこれから「aについて解く」わけですから2bを右に移項する必要があります。
移項する
移項とは、「符号を変えて=の向こうに移動させること」です。
符号を変えるのを忘れれば、答えを間違えちゃうので、気をつけてくださいね。
「a=」の式にする
aについて解かなくちゃいけないので、aの前にある3が邪魔ですね。
なので
3で割りましょう。
ここで3引いてしまう人がいますが、3aは3×aの略なので、3で引くことができません。
そうすると、
このように答えが表れます。
分数になると解けない理由
分数になった途端にめちゃくちゃ難しく感じてしまいますよね?
分数なんて日常生活で使うことがないので、ついつい問題を解くのを諦めてしまいます。
でもこの等式の変形は一つずつ手順を踏めば、必ず解けます
わからなくなったらこのサイトに戻ってきてやり方を思い出してください。
分数を使った等式変形のと解き方まとめ
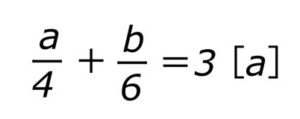
- 2つ(もしくは3つの分数)の最小公倍数をかける
![]()
- 左の辺(=の左側)から邪魔な項を移行させる
- aの前についてる数で割る
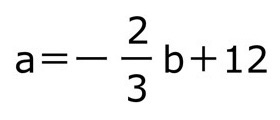
この3つの手順で解くことができます。
ぜひこの手順を覚えてやってみてください。
解き方の記事は他にもあるので、参考にしてみてください。
【中学数学】因数分解を1問10秒でこなす解き方と考え方
【一次関数】直線の式を求め方・解き方が超カンタンにわかる方法(動画アリ)
演習問題
次の方程式を解いてみましょう。
\(\displaystyle x=\frac{x}{3}\ + \frac{1}{4}\)
では、一度問題を解いてみましょう。
掛けてみてください
解法 & 解説
\(\displaystyle x × 12 =\frac{x}{3} × 12\ + \frac{1}{4} × 12\)
これを計算すると、\(\displaystyle 12 x = 4x + 3\)となります。
では、これを最後にまとめると
\(\displaystyle 8 x = 3\)となりますので、
結果 \(\displaystyle x = \frac{3}{8}\) となります。
付録
今回、小学生の時に習った、最小公倍数を使いました。あれは、ややこしいですよねぇ、私も嫌いでした。ただ、等式変形では「最小公倍数」が出てくるので最小公倍数の復習をしておきたいと思います。
問題:4 と 26 の最小公倍数を求めてみましょう。
では順番に倍数を出していきましょう。
| 整数 | 倍数 |
| 4 | 4,8,12,16,20,24,28,32,36,40,44,48,52,56,60,…. |
| 26 | 26,52,78,… |
この倍数の中で、もっとも小さい公倍数はというと「52」となります。
では、続いて3 と 18 の最小公倍数を求めてみましょう。
| 整数 | 倍数 |
| 3 | 3,6,9,12,15,18,21,24,27,30,33,36,…. |
| 18 | 18,36,54,… |
これは出来ましたか?「18」ですね。では、最後の問題に移りましょうか。
6 と 27と18 の最小公倍数を求めてみましょう。みっつですね。
| 整数 | 倍数 |
| 6 | 6,12,18,24,30,36,42,48,54,60,66,… |
| 27 | 27,54,81,… |
| 18 | 18,36,54,… |
つまり、答えは「54」となります。でも、これを全部考えるのは難しいです。もし、この先の解き方が出来そうな方は、次の解き方にもチャレンジしてみてください。
まず、各数字の掛け算の形に戻します。(割り切る事が出来ない一番小さな整数まで分けてもらいたいです。)
| 整数 | 掛け算の式 |
| 6 | 2×3 |
| 27 | 3×3×3 |
| 18 | 2×3×3 |
最小公倍数を作るルールがあります。それは、「全ての要素を掛け算すると最小公倍数が出来る」というルールです。
例えば、今回であれば
| 整数 | 掛け算の式 | 整数の数 |
| 6 | 2×3 | 2が1つ,3が1つ |
| 27 | 3×3×3 | 3が3つ |
| 18 | 2×3×3 | 2が1つ,3が2つ |
これらで構成されています。これらの要素を全て掛けて最小公倍数を作るというのは
「3を3つと、2を1つ掛け算する」というようにする事で、最小公倍数が出来ます。
今回であれば、3×3×3×2をすると最小公倍数が出てきます。
答えは「54」になります。