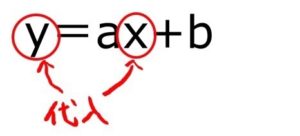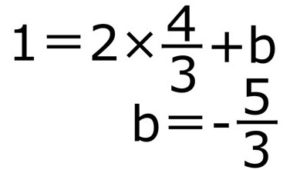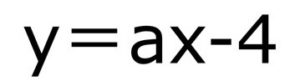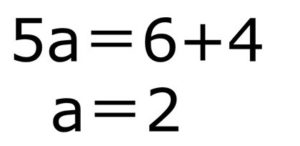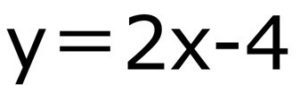中学の数学でよくつまづいてしまうのが一次関数です。
- 関数って何?
- 2点を通る直線の式?
- グラフを書け?
など疑問だらけの単元です。
「直線の式を求めよ」という問題で頭を抱えてしまう人は多いはずです。
なので、今回は一次関数の解き方について解説していきます。
わかりやすく一次関数の解き方を解説
直線の式を求めるときはいつでも 「\(\displaystyle y = ax + b\)」
ほんとこれだけ覚えてください。笑
直線の式とか、一次関数の式と言われたら問題の下にまず「\(\displaystyle y = ax + b\)」と書いてください。
一次関数 式 という単語が出たらすぐ「\(\displaystyle y = ax + b\)」です。
これを100回は口に出してください。
それくらい重要なことです。
今日はこれだけ覚えていってもらえたらいいです。
2点を通る直線の式を求める問題
直線の式を求める問題ですから、「\(\displaystyle y = ax + b\)」を書きます。
2点を通るということは、この2つの点の座標を代入してもいいってことです。
通る=代入してOKという意味です。
なので
2つの式ができます。
あとは連立方程式を使って
aとbが出ます。
したがって求める直線の式は
ですね。
そこまで難しく感じませんよね?
でも大事なのは、今わかることじゃなくて実際にテストで出て解けるようにする。
コレができるようにしましょう。
直線と平行なときの一次関数の式の解き方
こんな問題ですね。
まず何をするか。
もうわかりますよね?
、、、
そうです、式を求めるので「\(\displaystyle y = ax + b\)」です。
で、平行ということは傾きが同じという意味です。
傾きは覚えてますか?
ここのことですよ?
つまり、「\(\displaystyle y = 3x + 7\)」と平行なのでなので「\(\displaystyle y = 3x\)」の部分はわかりました。
よって求める直線の式は
「\(\displaystyle y = 3x + b\)」
となりますね。
問題には、点(3,5)と通るとありますね。
通るということは何でした?
覚えてますよね?
通る=代入してOK
つまり、「\(\displaystyle y = 3x + b\)」に代入すると
\(\displaystyle y = 3x + b\)
\(\displaystyle 5 = 3・3 + b\)
\(\displaystyle 5 – 9 = b\)
\(\displaystyle b = – 4\)
こうしてbが出ました。
なので求める直線の式は
「\(\displaystyle y = 3x – 4\)」
こうなるんですね。
切片だけがわかってる問題の直線の式の求め方
一次関数をやる上で重要な単語は、傾きの他に切片もあります。
なんとなく覚えてると思いますが、切片とはy=ax+bのbの部分ですね。
ではこの問題を解いてみましょう。
直線の式を求めるので、y=ax+bを出します。
もう言わなくてもわかりますね笑
そして切片が-4とわかっているので
となります。
そして点(5.6)を通る→代入してOK
整理すると、
a=2,b=-4とわかっているので、求める直線の式は、
となります。
どうでしょうか?
簡単に解けますよね
等式の変形の時も伝えましたが、数学は一個一個きっちりやれば必ず解けます。
ただやり方をよく覚えてなかったか、よく知らなかっただけなんです。
数学が嫌いとか苦手ではなく、ただ知らないだけ。
なのであなたも全然数学が出来るので一緒に頑張っていきましょう。
一次関数の式の解き方のおさらい
- 直線の式と言われたら迷わず「\(\displaystyle y = ax + b\)」
- 点を通るは代入してOK
- aとbを求めたら、それを「\(\displaystyle y = ax + b\)」に当てはめるだけ
- 傾きは「a」、切片は「b」
- 平行と言われたら傾きが一緒
ちょっと多いかもしれませんが、必ず覚えておいてください。
特に「直線の式を求めよ」と言われたら「\(\displaystyle y = ax + b\)」というのはめちゃめちゃ重要です。
墓場まで持っていってほしいくらい大事なものなので、これだけは覚えてください。
では、下に問題と答えを用意しておきます。
ですので、今日の復習に使ってください。
ちょっとわからなかった人や、忘れてしまった人はもう一度読み返してください。
またわからなくなればココに戻ってもらえればいいので、いつでも利用してください
解説してほしい単元があれば、コメント欄からお願いします。
- 【中学数学】因数分解を1問10秒でこなす解き方と考え方
- 【中学数学】「一次関数がわからない」が5分で解決するたった3つのポイント
- 手順はたった2つだけ!すぐわかる多項式の加法と減法の解き方
- そろそろ中学生は中間テスト!!数学は対策して攻略する!!
- 【中学数学】数学は計算だけではない!!「図形の証明」は得点源にしておかなければ受験は勝ち残れない!!確実に勝ち取る数学証明術
- 問題ページ