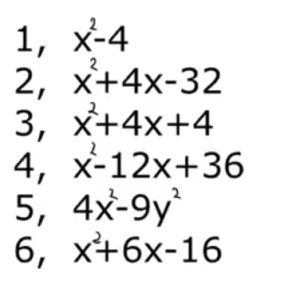因数分解??
中学3年生でやる因数分解(いんすうぶんかい)
なんだが言葉を聞くだけで難しそうな問題ですね笑
でも安心してください!
全然わからないって人でも計算の仕方も解き方のコツさえ知ればカンタンに解けるようになります。
ではやっていきましょう。
因数分解ってどういう意味?
因数分解はその通り、因数に分解するってことです!笑
もっとわかりやすくいうと、因数分解=かけ算の形にすることです。
例えば、
\(\displaystyle x^2 + 5x + 6 = (x + 3)(x + 2) \)
このように(x+2)と(x+3)のかけ算にすることです。
文字だとわかりにくいかもしれませんが、
12を2×6の形にすることと思えばわかりやすいですよね?
因数分解の単元の前に展開ってやりましたよね?
展開と逆のことをするのを因数分解とも言います。
とにかくかけ算の形にすること。それが因数分解です。
展開 ⇔ 因数分解
因数分解の公式の解き方
因数分解は公式がありますが、どの公式を使えばいいのか
ってところが一番難しいと覆います。
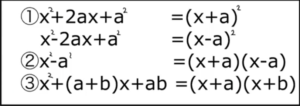
どの公式を使えばいいのかは、まず項の数をみます。
項とはx2+3x+2でいう 「x2」、「+3x」、「+2」のかけ算だけで表された式のことです。
この項が2つであれば、②の公式を使う可能性が大
項が3つであれば①か③どちらかを使う
まずこれを知っておいてください。
これを知っておくだけでも解くスピードがいつもの半分になります。
そして項が3つの場合どちらを使うか判断するポイントは、一番後ろの数です。
- x2+8x+16 ←この式の場合、16ですね。
- x2-6x+9 ←この式の場合の9です。
この一番後ろの数が整数の2乗の場合、①を使う可能性大です。
この場合、1,2ともに「整数の2乗」なので、①を使いますね。
| 一番後ろの項 | 2乗の整数 | |
| 1 | 16 | 42 |
| 2 | 9 | 32 |
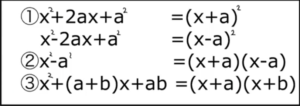
そうじゃなければ、9割くらいの確率で③の公式を使います。
項が3つ→1番後ろの数を見る→それが1、4、9、16、25、、、のように整数の2乗なら①の公式です。
これ覚えてしまえば、結構さくっと因数分解が解けちゃいます。
大事なのでもう一回言います
因数分解するときは何を見るんでしたっけ?
そうです、項の数です。
項の数が2つなら?
そう②の公式ですね。
項の数が3つなら①か③です。
| 項の数 | 公式番号 |
| 項が二つ | ② |
| 項が三つ | ① or ③ |
で、一番最後の数字が何になれば①の公式を使うんでしたっけ
「整数の2乗!!」
ってちゃんと心の中ですぐ答えられるようにしてくださいね。
項が3つで一番後ろが整数の2乗でなければ、③の公式を使いましょう。
とりあえず公式を覚えるかは置いといていいのでまず因数分解のどれを使うか、
それを見極められるようにしておきましょう。
ポイントは、項の数と一番後ろの数が整数の2乗かどうかですよ?
正直公式なんか覚えるよりどの公式を使うかわかる方が10倍大事です。
公式覚えたらできるよ!なんて嘘です笑
解き方を知ればできるんです!!!
どの公式を使うか3秒でわかるかゲーム
僕はよくこのゲームをします。
問題を指差して、①②③どれを使うか答えてもらうのです。
最初は反応が遅いですが、やればやるほど早くなります。
そしてちょっとおもろいです笑
では問題を見てみましょう。
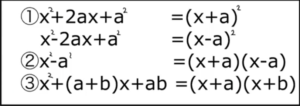
上から順に何番の公式を使うか言ってみてください。
いいですか?
3秒以内で答えられるよう頑張る、
それがこのゲームのポイントです!
もちろん最初は何秒かかっても大丈夫です。
でもテスト直前には3秒で答えられるように訓練しておいてください。
では、いきましょう。
①の問題から、
- ②の公式使う
- ③の公式使う
- ①の公式使う
- ①の公式使う
- ②の公式使う
- ③の公式使う(これはちょっと特殊かもしれません。)
こんな風にまず考えます。
公式を覚えるのは、これが出来てからでいいです。
なんでもかんでも公式覚えればできるわけじゃないのが数学です。
めんどくさいですね笑
最後の問題だけがちょっとイレギュラーかもしれませんが、これで因数分解はできますよね?
コツさえ教えてもらえれば、出来るようになる!
これが数学です。
ちなみに答えは、上から
- (x+2)(x-2)
- (x+8)(x-4)
- (x+2)2
- (x-6)2
- (2x+3y)(2x-3y)
- (x+8)(x-2)
です。
今日はどの公式を使うかわかるようになる。
これが目標なので、どの公式を使うかわかるようになれればOKです。
では、③の公式について説明していきます。
③の公式「x2 +(a+b)x -ab =(x – a)(x + b)」は、
真ん中の項(a+b)→ 足し算
一番後ろの項 ab → 掛け算
となっている事がわかります。
つまり、因数分解を解法する上で必要になる二つの整数は、
真ん中の項(a+b)→ 二つの整数を足し算し
一番後ろの項 ab → 二つの整数を掛け算している。
という事になるわけです。
例えば、6番目の問題 x2 +6x -16を因数分解してみます。
| 真ん中の項 → 足し算 | 一番後ろの項 → 掛け算 |
| 足して +6 | 掛けて -16 |
になる、二つの整数を探します。
まず、掛けて -16なので、
| 整数1 | 整数2 | |
| 1 | -16 | 1 |
| 2 | -8 | 2 |
| 3 | -4 | 4 |
| 4 | -2 | 8 |
| 5 | -1 | 16 |
となるのですが、この中から「足して +6」になる整数の組み合わせを探してみます。
| 整数1 | 整数2 | 足し算 | |
| 1 | -16 | 1 | -15 |
| 2 | -8 | 2 | -6 |
| 3 | -4 | 4 | 0 |
| 4 | -2 | 8 | +6 |
| 5 | -1 | 16 | +15 |
この結果、表の4番目の整数の組み合わせが「+6」となるため、6番目の因数分解の解答は
x2 +6x -16 =(x – 2)(x + 8)となります。
少し工夫が必要ですが、そこまで難しくはないので
慣れるまでは繰り返し問題を解いてみてください。
因数分解をミスゼロで素早く解く方法おさらい
おさらいをしましょう。
項の数→2つなら②の公式
項の数→3つなら①か③
一番後ろの数が整数の2乗なら①
そうじゃなければ③の公式
ほんとにこれを覚えるだけでいいです。
公式よりもこれを覚えて帰ってください。
使い方がわかれば、公式も覚えやすくなるのでまずこれを頭にインストールしてください。
これが因数分解をできるようになるための一番早い解き方です。
ダマされたと思って、覚えていってください。
因数分解と聞けば、すぐに
「項の数と一番後ろの数字を見る」
これが思い浮かぶようになれば、あなたも因数分解マスターです!!
そして、③の公式を使う問題を解くときは、
③の公式「x2 +(a+b)x -ab =(x – a)(x + b)」は、
真ん中の項(a+b)→ 足し算
一番後ろの項 ab → 掛け算
です。これで確実に問題を解くことはできます。
テストでも全然わからない。
なんてことは絶対に起こらなくなります。
今回は以上です。
ちゃんとわかるようになってからこのページを閉じてくださいね。
追記ですが、定期テストや受験でもしっかり出てきます。受験であれば、公立高校を受験する場合でも、私立を受験する場合でも、必ず登竜門のように問題は出てきます。しっかりマスターしてテストの時に抜けのないようにしておくと心強いと思いますよ。
展開について(付録、時間があれば見てください)
「展開」と「因数分解」はテストでよく出てくる範囲です。ここでは、「展開」についても触れておきたいと思います。
例えば、次のような問題を見てみましょう。
下記の式を展開しなさい。
\(\displaystyle (x + 3)(x – 2) \)
この式を展開する時ですが、分配法則を使って、一つずつ「カッコ」を外していきます。\(\displaystyle (x + 3) \) を \(\displaystyle (x – 2) \) に分配していきます。
\(\displaystyle (x + 3)x – (x + 3)2 = x(x + 3) – 2(x + 3) \)
このようになるはずです。続いて、\(\displaystyle x(x + 3) – 2(x + 3) \)を展開していきましょう。
| 展開前 | \(\displaystyle x(x + 3) \) | \(\displaystyle – 2(x + 3) \) | ||
| 展開後 | \(\displaystyle x^2 \) | \(\displaystyle 3x \) | \(\displaystyle – 2x \) | \(\displaystyle – 6 \) |
これらをつなげると\(\displaystyle x^2 + 3x -2x – 6 = x^2 + x – 6 \)となりました。これで展開は完成です。
でも、この展開の式を見てほしいです。
\(\displaystyle (x + 3)(x – 2) = x^2 +(3 -2)x – 6 = x^2 + x – 6 \)は、因数分解の③の公式の逆バージョンでしょ?最初の方でもお伝えした通り、
展開 ⇔ 因数分解
なので、因数分解を習得するためには、展開の計算は必須です!展開の計算が出来れば、因数分解は楽勝です!
この後に出てくる、
「ルート計算」「二次方程式」「二次関数」
でも使う事になるので、因数分解と展開は絶対出来るようになっておくといいですよ!!
数学に関する関連記事はこちらです。
【一次関数】直線の式を求め方・解き方が超カンタンにわかる方法(動画アリ)
【3分でわかる】分数を使った等式の変形の解き方
手順はたった2つだけ!すぐわかる多項式の加法と減法の解き方
【中学数学】文字の代入計算、計算ミスを起こしやすい問題が多い単元は、受験生がみんな失点する。確実に物にすると得点源に