
こんな悩みに答えます。
この記事の内容
- 【数学】図形の証明について
- 【数学問題】簡単な証明演習問題
- まとめ
みなさん、数学の証明って難しいとおもいませんか?図形の証明そのものが難しいのではなくて、いきなり計算ではない数学が出てくるのが証明問題です。
しかも、残念な事にこれから証明問題はどんどん増えてきます。
この証明問題について、これから確認していきましょう。
ここでしっかりマスターすれば、数学の証明は得点源になったも同然です!!
【数学】図形の証明について

いきなりですが、証明の問題解いていますか?
ちょっと分からないから、計算問題だけ解こうとか、文章問題だけ解こうという具合に、問題を限定的に解いてはいませんか?

駄目ですよ!計算問題だけにしていては。
数学の受験問題には必ずと言って良いほど「図形の証明」の問題が出てきます。
なので、この「図形の証明」の問題を捨ててしまうと、後で必ず後悔することになってしまいます。そこで、今回は「図形の証明」の問題を解くにあたって重要なポイントを押さえていきます。
では、今回は三角形の証明問題から見ていきます。まず、合同条件を確認してみましょう。
- 三組の辺が等しい
- 二組の辺とその間の角が等しい
- 一組の辺とその両端の角が等しい
そもそも、証明とは何か?というと
二つの図形が、互いに同じ形ですよ、という事を文章で説明して、証明する事!!
こういう説明です!じゃぁどうやって説明しますか?それは先ほど書きました
「合同条件」
に当てはめながら、説明をしていくという事になります。

と、悩むと思いますが、例えば、
今回は「三角形の合同条件」を三つお伝えしています。
この「三角形の合同条件」というのは「二つの三角形が同じですよ」というルールです。なので、このルールを覚える事が、証明の問題を解く第一歩になります。
それでは、問題を一緒に解いてみましょう。
△ABC と △DEFが次の条件をみたすとき、△ABC ≡ △DEF であるといえますか。また合同であるとき、その根拠となる合同条件を答えなさい。
AB = DE , BC = EF , ∠B = ∠E
このような問題です。
まず「≡」 ← これは「合同」という意味です。
つまり、今回は△ABC と △DEFが合同ですか?という問題です。
では、図を使って整理しておきましょう。

このような、図の形になります。もちろん形も同じなので、
「合同で良いんじゃね?」
みたいに思うかもしれませんが、それでは問題になりません。ここにはちゃんと理由が必要になります。
まず、この問題には「お互いの辺が等しい」や「お互いの角が等しい」など、図形が等しいというための材料が文章中にあります。
- AB = DE
- BC = EF
- ∠B = ∠E
この三つの材料ですが、これが合同かどうかを判断するための基準になります。先ほどの図をもう一度みてみます。

これは、「二組の辺が等しくて、その間の角も等しい」となるわけですから、
条件でいうと、「二組の辺とその間の角が等しい」という事になるわけです。という事は、この条件にはまっている「△ABC と △DEF」同じ三角形という事なので、
「△ABC ≡ △DEF」となるわけです。
難しくはないと思いますが、なんかフワッとしている感じだと思うので、次は演習問題で一度問題を解いてみてください。
【数学問題】簡単な証明演習問題
△ABC と △DEFが次の条件をみたすとき、△ABC ≡ △DEF であるといえますか。また合同であるとき、その根拠となる合同条件を答えなさい。
AC = DF , ∠A = ∠D , ∠C = ∠F
この問題を解くにあたって、先ほどもお話した「三角形の合同条件」のどれに当てはまるのかを確認する必要があります。これをしっかり理解したうえでこの問題を解いてみましょう。
解答 & 解説
今回の問題を図に表してみます。
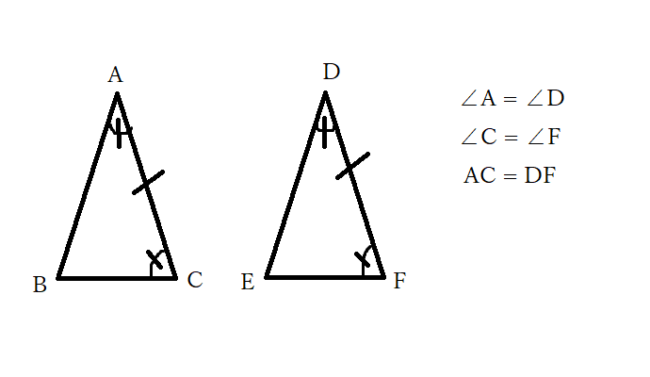
前回の問題と違う点としては、一組の辺だけが等しく、その両端と角度が等しくなっているという所です。このような、合同条件はあるでしょうか?もう一度先ほどの三角形の合同条件を見てみましょう。
- 三組の辺が等しい
- 二組の辺とその間の角が等しい
- 一組の辺とその両端の角が等しい
3番目に「一組の辺とその両端の角が等しい」という条件がありますね。
ということは、今回の問題も、「一組の辺とその両端の角が等しい」という条件を満たしているので三角形の合同は証明されたという事になります。
まとめ
三角形の証明の問題は、もう少し突っ込んだ問題が出てきますが、一番大事な基本を押さえてください。特に、
- 三組の辺が等しい
- 二組の辺とその間の角が等しい
- 一組の辺とその両端の角が等しい
この条件は受験の時の、穴抜きフレーズとして出てくる事があります。穴抜きフレーズで出てくるという事は、この文章を書けるようにしておかなければならないので、受験対策として覚えておいた方が良いので、絶対に暗記しておいてください。これから志望校を決めていくにあたり、中学3年生は実力テストを受けていく時期になると思いますが、証明は必ず出てきます。数学の点数をアップさせるために、計算問題と証明問題を解くことができれば、60点は固いです!!確実に点を稼いで、第一志望合格をつかんでください!!


