だいぶ問題対策はできたけど、まだまだ心配です。

他にも対策できるものはあるので、他の対策も立てておきましょう。
この疑問に答えます。
この記事の執筆者はむーむーです。
この記事の内容
- 数学の問題の中には部分点が存在しているものがある。
- 部分点の例題をみてみよう。
- まとめ
計算問題も標準単元問題も、できる所は対策したけどまだまだ不安材料がいっぱいという方が多いと思います。応用問題に手を出そうか、発展問題に手をだそうか、色々な問題の対策を幅広くしておくべきか、考えだしたらきりがありません。もちろん全部出来るならしておきたいですが、色々な問題に手を出し過ぎて沼にはまる事が多いので、ここは取捨選別して対策を立てるようにしておく
数学の問題の中には部分点が存在しているものがある。
中学生で習う数学の問題は一問一答形式で、問題に対して必ず答えがあるものが多いと思います。今まで解いてきた計算問題や標準単元問題など、必ず答えが一個に決まるケースが多かったはずです。しかし、数学にも唯一部分点が存在している問題があります。それが証明問題です。証明問題には、図形、計算式、説明など様々な形式のもがありますが、それら大体部分点があります。そのため証明の問題は完璧を目指さずに、おおまかに7から8割を目指す、もし解く事が出来なければ分かる所だけ書く!これを心にとめながら問題を解くようにして下さい。
図形の合同証明
オーソドックスな三角形合同証明問題
三角形合同証明問題は、呪文のように覚えた3つの定義があったと思います。
- 3辺がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 1辺とその両端の角がそれぞれ等しい
三角形合同証明問題はこのみっつのどれかが必ず当てはまります。そのため、この3つは100%覚えておいてください。
では、配点踏まえてサンプル問題を解いていきましょう。例えば証明で10点問題を作ってみます。
サンプル問題(三角形合同証明)
次の図形のうち、辺AB=辺CDである事を証明してください。(10点)
条件:辺BO=辺DO、辺AO=辺CO
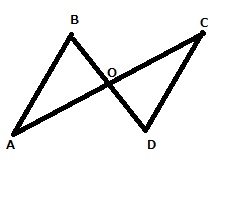
この三角形の証明は、非常にオーソドックスな証明の問題です。証明の記述方法としては、
△ABOと△CDOにおいて
仮定より、(条件が最初から用意されている時は、仮定よりと記述し始める)
辺BO=辺DO・・・①
辺AO=辺CO・・・②(あとで証明をするために使う要素は、①、②と数字を振る)
—–ここまでで2点——
対頂角より、(角と角が向いあっている状態が対頂角、対頂角は同じ角度である。)
∠AOB=∠COD・・・③
—–ここまでで2点—–
①、②、③より
2辺とその間の角がそれぞれ等しい(ここに該当する条件を入れる)
—–ここまでで2点—–
よって、△ABO≡△CDO(ここで大事なポイントは三角形が合同だから、辺は同じでしょ?という事が言いたいので、これだけで証明を終わらせない!)
—–ここまでで2点—–
ゆえに、辺AB=辺CDである。(ここまで書ければ正解!)
—–ここまでで2点—–
以上が、証明問題の証明記述です。このタイプの問題は出やすい、むしろ場合によっては受験で普通に出てくるので、出来るようにしておくと得点源になります。仮に証明が分からなかったとしても、仮定と結論を書く事が出来れば4点取れるので、試験中に時間が無くなってしまっても、仮定と結論だけでも書くようにしておきましょう。
図形の相似証明
相似とは
相似の問題も良く出てくる問題です。
相似は、合同と違い三角形の形が同じかを証明するものです。三角形の相似条件を三つおさえておきましょう。
- 3組の辺の比がすべて等しい。
- 2組の辺の比が等しく、その間の角が等しい。
- 2組の角がそれぞれ等しい。(☆)
特に☆マークを付けた、「2組の角がそれぞれ等しい」はかなり重要な要素で、どこでも使う事が出来る万能ツールなので、覚えておくと絶対損しないはずです!
次回は、相似証明問題を実際に対策してみたいと思います。
まとめ

三角形の合同証明かぁ、久しぶりに解いた気がする!

証明問題で部分点を稼げるようにしておくと良いですね!
今回は、公立高校入試直前対策で部分点を稼ぎやすい証明問題を見て頂きました。特に合同証明は、中学二年生の時に苦戦した方が多いのではないでしょうか。この手の問題は試験委員は非常に大好きな問題です。ただ、証明の問題には唯一部分点が存在している事は忘れないようにしておいてください。部分点がある事が分かれば、解答用紙真っ白で出さなくて済みます!例え1点でも、受験の1点凄く大きい1点です。
なのでおさらいですが、
図形の合同証明条件
- 3辺がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 1辺とその両端の角がそれぞれ等しい
図形の相似証明条件
- 3組の辺の比がすべて等しい。
- 2組の辺の比が等しく、その間の角が等しい。
- 2組の角がそれぞれ等しい。(☆)
特に☆マークは良く出るので、忘れないようにして下さい!
次回は、相似証明の問題について見ていきましょう!