せんせー、そうじ?って何ですか?

相似は証明の一つです!かなり重要ポイントの一つなので、覚えておきましょうね。

合同とか相似とかよく分からないけど、前回の合同は何とかマスターしたので、あと少しなので頑張ります!

良く似た条件ですが、覚えてしまえば楽勝なので、ぜひチャレンジしてください!
この疑問に答えます。
この記事の執筆者はむーむーです。
この記事の内容
- 図形の相似の証明について
- 相似条件はここだけおさえよう!
- まとめ
前回は、図形の合同条件について確認していきました。合同も3つ条件があるので、どれが出てくるか分からないと思う部分もあると思います。ですが、証明は部分点があるので、ある程度の型が分かれば、誰でもとける問題なので、型を覚えるようにしていくと良いと思います。
図形の相似の証明について
相似の証明は、合同と違って同じ三角形を証明するのではなく、大きさは違うけど、
「形は一緒です。」という事を証明するのが、相似の証明です。
合同の証明と違って、相似は形が一緒を示すだけなので、そこまで厳密な条件定義をしなくてもいいというのが、相似の証明の良い所です。
一度条件の確認をしてみたいと思います。
相似の証明の条件について
三つの条件
前回もお伝えしたものですが、入試には相似の証明は良く出てきます。そのため、特に三角形の相似条件を三つおさえておきましょう。
- 3組の辺の比がすべて等しい。
- 2組の辺の比が等しく、その間の角が等しい。
- 2つの角がそれぞれ等しい。(☆)
☆マークの条件は良く使います!凄く使います!証明でなくても使うので、ぜひ覚えておきましょう。
三角形の相似に関する問題を解いてみよう!
以下の問題の証明を解いてみましょう。
条件:AC//DB
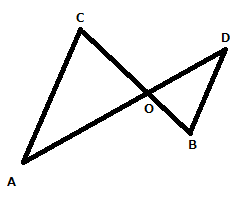
相似の証明の解き方
もうお分かりですよね?そうなんです。
この証明の条件は☆マークの所でお伝えした、
- 2つの角がそれぞれ等しい。(☆)
これしか使いません!合同の証明であれば長々と証明する必要があるのですが、相似は凄くシンプルです。二つの角がそれぞれ等しければ、証明完了なんですね!
では、早速証明を解いていきましょう。
△AOCと△DOBにおいて、
AC//DBの条件より、平行線の錯角から
∠ACO=∠DBO(錯角)・・・①
∠CAO=∠BDO(錯角)・・・②(これでほぼ完了です。あとは条件を定義していきましょう。)
①、②より
2つの角がそれぞれ等しいので、
△AOC∽△DOBとなる。
凄くシンプルな証明になります。なので、相似の条件は「2つの角がそれぞれ等しい」をぜひ覚えておいてください。色々な所で活用できるツールですので!!
まとめ

なんか今日はあまり勉強したって感じがしないけど、凄く得した気分!

相似の証明は、凄く難しく見えて、実は型が決まっているので、そこまで難しくならないです!それに、よく出てくるのが相似です!

そんなに出るなら相似だけ勉強すれば良いのに。。。。

そうやって相似だけやってると、合同証明が出た時に足元をすくわれるので注意しましょう!!

はーい。
どうだったでしょうか?直前の対策なので、あまり深い所までは相似の証明はしていないですが、それでも2つの角がそれぞれ等しいは良く出てきます!高校の学習の中でも出てくる事が多いので、そこは油断せず学習を進めるようにしていきましょう!