
せんせー、平行四辺形って証明条件とかありますか?

平行四辺形の証明条件はちゃんとあります!

でも見たことないかも。。。

ではこれから説明するので、しっかり覚えてください。
この疑問に答えます。
この記事の執筆者はむーです。
この記事の内容
- 平行四辺形の証明について
- サンプル問題を紹介
- まとめ
三角形の合同証明条件は、よく出てきますし、皆さんもよく知っていると思います。ただ意外と手薄になるのが、平行四辺形の証明です。平行四辺形の証明条件はそんなに難しいものではないので、確実にマスターしておくと良いでしょう。
平行四辺形の証明について
平行四辺形の証明は、頻繁に出てくる問題ではないですが、問題の中で
「この図形はどんな図形ですか?」
と問われるケースの問題に平行四辺形が良く出てきます。そのため、その図形が平行四辺形と断定するための条件をおさえておけば、「どんな図形問題」は攻略できるので、平行四辺形の条件は確実に頭に入れるようにしておいてください。
平行四辺形の証明条件
平行四辺形の証明条件は五つあります。
- 2組の向かい合う辺(対辺)がそれぞれ平行である。
- 2組の向かい合う辺(対辺)がそれぞれ等しい。
- 2組の向かい合う角(対角)がそれぞれ等しい。
- 対角線が、それぞれの中点で交わる。
- 1組の向かい合う辺(対辺)が平行で、その長さが等しい。
このうちどれかが成り立てば良い!
このうちどれか1つが成り立てば、平行四辺形になります。
もちろん条件なので、全て知っておく必要があります。しかし、当てはめる条件は一つだけなので、仮に一つの条件がはまっていれば、その図形は平行四辺形という事になります。
条件の内容も、条件の1~3については、そこまで難しくないのでサラっと流してもらって大丈夫だと思いますが、条件4,5については見覚えがないと思うので、特に条件4,5について詳しくみてみこうと思います。
平行四辺形サンプル問題
対角線が、それぞれの中点で交わる。
条件4の「対角線がそれぞれ中点で交わる。」タイプの問題を見ていきましょう。
問題
次の図形は、どんな図形ですか?
条件:AO=DO、BO=CO
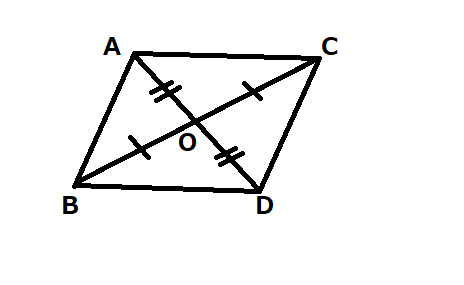
この図形の条件から、
「対角線がそれぞれの中点で交わる」という条件を満たしている事が確認できると思うので、この図形は「平行四辺形」と断定できます!
証明の問題というのは、どうやって自分が考えている図形や条件と「決めつける!」事が出来るかという問題です。どれかの条件に当てはまれば、その図形と決めつける事が出来るので、難しく考えずに取り組んでもらえると良いかもしれません。
1組の向かい合う辺(対辺)が平行で、その長さが等しい。
次は条件5の「1組の向かい合う辺(対辺)が平行で、その長さが等しい。」タイプの問題を見ていきましょう。
次の図形はどんな図形ですか?
条件:AD//BC、AD=BC
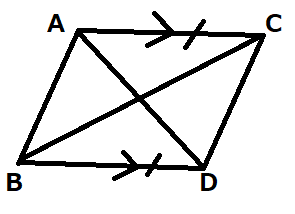
もう分かると思います。この図形の条件から、
「1組の向かい合う辺(対辺)が平行で、その長さが等しい。」という条件を満たしている事が確認できると思うので、この図形は「平行四辺形」と断定できます!
ここで注意が必要なのが、1組の辺が平行かつ長さも等しいという事です。ここは両方の条件を満たさないといけないので、1組だけで平行四辺形を証明する時は、平行かつ長さも等しいを忘れないようにして下さい。
挑戦!証明問題(平行四辺形編)
次の図形は、どんな図形ですか?証明を交えてその図形を答えてください。
条件:AC=BD、∠CAD=∠BDA
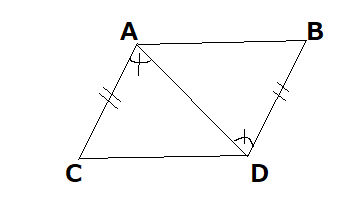
では、証明していきたいと思います。
順番としては、
- 三角形の合同の証明をする。
- そして、平行四辺形の条件に当てはまるものを探す。
- 条件より証明する。
△ACDと△ABDにおいて
仮定より、
AC=BD・・・・①
∠CAD=∠BDA・・・・②
そして、AD=DA(共通)・・・・③
①、②、③より
「二つの辺とその間の角が等しい」ので
△ACD≡△ABDとなる。
ゆえに、AB=CD・・・・④
①、④より
2組の向かい合う辺(対辺)がそれぞれ等しい。(条件2が使える!)ので、
四角形ABCDは平行四辺形である。
ここまでできれば、平行四辺形の証明は完璧です!
難しいように見えますが、順番は
- 三角形の合同の証明をする。
- そして、平行四辺形の条件に当てはまるものを探す。
- 条件より証明する。
となるので、しっかりセオリーをおさえてチャレンジしてください。
まとめ

平行四辺形は結構楽勝かもしれない。

確かに楽勝ですね!ただあなどると落とし穴が待っているので、気を引き締めてチャレンジしてください。
いかがでしたか?平行四辺形の証明は、あまり身近には出てこないかもしれませんが、出てくると厄介な問題です。しかし、条件をおさえるとそこまで難しい問題ではないので、五つの条件はさらっと確認しておくと良いでしょう。
そして、どのような証明の問題も、最初は「三角形の合同証明」がスタートです。もちろんそうでない問題もありますが、大体の問題が三角形の合同証明をしてから、平行四辺形に移ったりする事が多いので、まず条件として何が必要になるのかを考えながら証明問題を進めるとよいでしょう。

